2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
문제
문제
두 전봇대 A와 B 사이에 하나둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
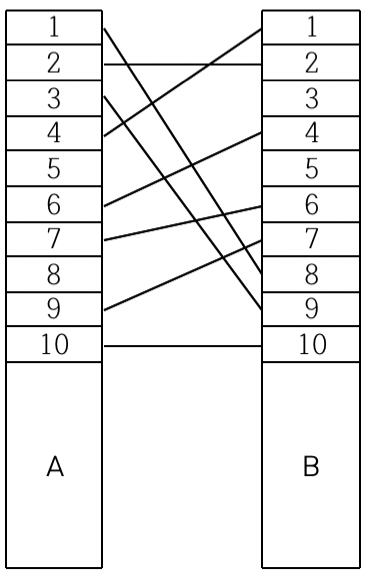
< 그림 1 >
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
예제 입력 1 복사
8
1 8
3 9
2 2
4 1
6 4
10 10
9 7
7 6
예제 출력 1 복사
3문제 풀이
처음 접근할 때 겹치는 부분을 수열로 저장하여 가장 많이 겹치는 전깃줄부터 하나씩 없애는 것을 겹치는 전깃줄이 없을 때까지 반복하여 구현하려 했다.
우선 이 방법은 구현 자체가 까다로우며 실행 시간이 오래 걸릴 것으로 생각이 됐다.
겹치는 정도를 나타내기 위해 겹치는 전깃줄들을 배열로 따로 저장을 할 경우 완전탐색을 통해 없앤 전깃줄과 겹치는 전깃줄들의 배열에서도 없애줘야 하기 때문이다.
또한 정확도에서도 문제가 발생할 것 같았는데, 같은 갯수만큼 겹치는 전깃줄 중 어느 것을 없애야 결과적으로 이득이 될지는 알 수 없었다.
이 방법은 운이 좋게 통과된다고 하더라도 입력의 크기가 조금만 커져도 통과하지 못하겠다 싶었다.
따라서 다른 방법을 생각해 보았다.
그림을 살펴보자

전깃줄을 A의 위에서부터 아래로 차례대로 살펴 볼 때,
겹친다는 것의 정의를 다르게 생각해 보면 앞서 나오는 전깃줄이 뒤에 나오는 전깃줄보다 종착지가 아래라는 점이다.
종착지 B에서 아래에 존재하는 전봇대는 위에 존재하는 전봇대보다 수 자체가 크므로 종착지의 크기가 얼마나 큰지를 비교하여 이전보다 위에 존재하는지 아래에 존재하는지 알 수 있다.
이를 응용하여 이 문제는 연속해서 가장 긴 연속하는 수열의 길이를 찾게 되면 그 수열의 길이가 전깃줄을 최소로 제거하여 만들 수 있는 가장 최선의 결과이다.
가장 긴 연속되는 수열의 길이를 찾기 위해서 완전 탐색도 가능하겠지만 다이나믹 프로그래밍을 통해 빠른 시간 내에 해결할 수 있다.
다이나믹 프로그래밍으로 구현하기 위해서는
각 수열의 크기를 저장하는 배열(A)과,
해당 수열까지의 연속되는 수열의 길이를 저장하는 배열(B)이 필요하다.
크기를 저장하는 배열은 input으로 들어오게 되므로 연속되는 수열의 길이를 저장하는 배열을 만들기만 하면 된다.
임의의 수[i]의 연속되는 길이를 저장하기 위해 다음과 같은 전제조건이 필요하다.
1) B[i]에 저장되는 값은 A[i]를 포함하는 수열의 가장 긴 길이이다.
2) B[i-1]까지 이미 계산이 완료되어 있다.
저장하는 과정을 살펴보자
A의 i번째 수를 포함하는 수열의 가장 긴 길이는 A[i-1]까지의 수열들 중 A[i]보다 작으면서 B의 같은 위치에 저장된 가장 큰 수 + 1 이다.
그림과 같이 살펴보자
수열의 크기를 저장하는 배열 A
A[i]까지의 수들 중, A[i]를 포함한 부분수열 중 가장 긴 오름차순 부분수열의 길이를 저장하는 B라 할 때,

이렇게 저장이 된다.
구현 방법
먼저 랜덤하게 들어오는 전깃줄에 대한 정보들을 시작점을 기준으로 정렬한다.
B를 A의 길이만큼 1을 갖는 배열로 초기화한다.
각 A를 살피며 A로 만들 수 있는 가장 긴 연속되는 수열의 길이가 얼마인지를 B에 저장한다.
B에 저장하는 알고리즘은 다음과 같다.
j= 0부터
1) A[j]의 크기와 현재 살펴보고 있는 수A[i]와 비교한다.
2) A[i]가 A[j]보다 크다면,
2-1) B[j] > B[i]일때, B[i] = B[j]
2-2) 나머지의 경우 A[j]를 포함하여 만드는 경우보다 더 나은 경우를 알고 있으므로 무시한다.
3) A[i]가 A[j]보다 크지 않다면, A[j]를 포함하여 수열을 만들경우 연속되는 오름차순 수열이 아니므로 무시한다.
4) j += 1 후, j < i인 동안 1~4)를 계속해서 반복한다.
코드
##A == graph
##B == dp
N= int(input())
graph = [list(map(int,input().split()))for _ in range(N)]
graph.sort()
dp = [1 for i in range(N)]
for i in range(N):
for j in range(i):
if graph[i][1] > graph[j][1] and dp[j] >= dp[i]:
dp[i] = dp[j]+1
print(N-max(dp))
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 1005-ACM Craft (Python) (0) | 2023.03.05 |
|---|---|
| [백준] 1744 - 수 묶기 (Python) (0) | 2023.03.01 |
| [백준] 14725 개미굴 (Python) (0) | 2023.02.19 |
| [백준] 11758 CCW (Python) (0) | 2023.02.18 |
| [백준] 15486 퇴사 2 (Python) (0) | 2023.02.18 |
